Advanced Topics

Guide

Advanced Topics

Laplace-Runge-Lenz Vector

For an inverse square law force of the form

\mathbf{F} = -\frac{k}{r^2} \hat{\mathbf{r}}

and the corresponding potential energy $V(r) = -k/r$ , the super useful Laplace-Runge-Lenz vector, or LRL vector is defined as

\tag{3.7.1} \boxed{ \mathbf{A} = \mathbf{p} \times \mathbf{L} - m k \hat{\mathbf{r}} }

$\mathbf{p}$ and $\mathbf{L}$ are the linear and angular momentum of the particle at any instant, and $\hat{\mathbf{r}}$ is the unit vector pointing from the center of mass to the particle. The constant parameter k describes the strength of the central force; it is equal to $GMm$ for gravitational forces. The LRL vector is a scaled version of the eccentricity vector, $\mathbf{A} = mk \mathbf{e}$ , and hence is a constant of motion. The magntidue of the LRL vector is

\tag{3.7.2} A^2 = m^2 k^2 + 2mEL^2

where E is the total energy of the system.

The Laplace-Runge-Lenz vector is a constant of motion for central force problems. (Source: Wikipedia)

Trajectory of the momentum vector

The conservation of the LRL vector $\mathbf{A}$ and angular momentum vector $\mathbf{L}$ is useful in showing that the momentum vector $\mathbf{p}$ moves on a circle under an inverse-square central force. The trajectory of the momentum vector $\mathbf{p}$ is called a hodograph.

mk \hat{\mathbf{r}} = \mathbf{p} \times \mathbf{L} - \mathbf{A}

\implies (mk)^2 = A^2 + p^2L^2 + 2\mathbf{A} \cdot (\mathbf{p} \times \mathbf{L})

Choosing $\mathbf{L}$ along the $z$ -axis, and the major semiaxis as the $x$ -axis, yields the locus equation for $\mathbf{p}$

\tag{3.7.3} p_x^2 + \left( p_y - \frac{A}{L} \right)^2 = \left( \frac{mk}{L} \right)^2

Thus, the momentum vector $\mathbf{p}$ is confined to a circle of radius $mk/L$ centered on $(0,\, A/L)$ . For unbounded orbits, $A > mk$ and hence the circle does not intersect the $p_x$ -axis.

The hodograph is a useful tool for visualizing the momentum vector in central force problems. (Source: Wikipedia)

Precession of LRL vector under a perturbed potential

Consider a small perturbation $h(r)$ to the potential energy $V(r)$ , such that

V(r) = -\frac{k}{r} + h(r)

Since the force is no longer inverse-square, the LRL vector is no longer conserved, and precesses, leading to precessiong of apsis.

\frac{d\mathbf{A}}{dt} = - \frac{d h(r)}{dt} \, \hat{\mathbf{r}} \times \mathbf{L} = L \frac{d}{dt} h(r) \: \hat{\mathbf{\varphi}}

Since $\mathbf{L}$ and $E$ are still conserved, the magnitude of $\mathbf{A}$ remains constant. Writing $L = mr^2 \dot{\theta}$ ,

\frac{d \mathbf{A}}{d \theta} = -m \frac{d}{du} h(u) \hat{\mathbf{\varphi}}

where $u = 1/r$ . The average precession of the apsis

\Delta \varphi \approx \frac{|\Delta \mathbf{A}|}{A} = \frac{m}{A} \int_0^{2 \pi} \frac{d}{du} h(u) d \theta

The rate of precession is therefore given by

\tag{3.7.4} \dot{\varphi} = \frac{m}{AT} \int_0^{2 \pi} \frac{d}{du} h(u) d \theta

If the perturbation is small, the orbit during one revolution can be approximated as keplerian

u = \frac{mk}{L^2} \left[ 1 + \frac{A}{mk} \cos \theta \right]

and hence the integral can be evaluated.

For example, the potential due to a point mass in general relativity is given by

\tag{3.7.5} V(r) = - \frac{GMm}{r} - \frac{GML^2}{mc^2r^3}

Evaluating the integral gives

\tag{3.7.6} \Delta \varphi = \frac{6 \pi G^2M^2m^2}{c^2L^2}

Orbit Equation

The energy of a particle of mass $m$ moving in a central potential $V(r)$ is

E = \frac{1}{2}mv^2 + V(r) = \frac{1}{2}m(\dot{r}^2 + r^2 \dot{\theta}^2) + V(r)

Differentiating with respect to time, and substituting the $L = mr^2 \dot{\theta}$ , we get the equaiton of motion of the particle

m\ddot{r} - \frac{L^2}{m r^3} = - \frac{dV}{dr}

Substituting $u = 1/r$ and simplifying, we get

\tag{3.7.7} \boxed{\frac{d^2 u}{d \theta^2} + u = -\frac{m}{L^2} \frac{d}{du} V(u)}

This is the orbit equation. Also referred to as Binet’s equation, it describes the shape of the orbit $r(\theta)$ of a particle moving under a central force. If the shape of the trajectory is known, the force law can be determined by solving for $V(u)$ .

For an inverse square force having potential $V(r) = -k/r = -ku$ , the orbit equation $u(\theta)$ is given by

\tag{3.7.8} \frac{d^2 u}{d \theta^2} + u = -\frac{km}{L^2}

This is, again, the equation of a conic section. The solution $u(\theta)$ is

u = \frac{mk}{L^2} \left( 1 + e \cos (\theta - \theta_0) \right)

where $e$ (the eccentricity) and $\theta_0$ (the phase offset) are constants of integration.

📍

Let us clarify what bound, closed and stable orbits mean

A bound orbit is one where the total energy $E < 0$ . The particle cannot escape to infinity, and will always remain within a certain distance from the center of force.
A closed orbit is one where the particle returns to its initial position after a finite period of time. Closed orbits are a subset of bound orbits, but not all bound orbits are closed. For example, in an inverse-square law force, elliptical orbits are closed, but parabolic and hyperbolic orbits are not.
A stable orbit is one where small perturbations to the particle’s position or velocity do not lead to large deviations from the original orbit. In other words, if the particle is slightly displaced from its orbit, it will oscillate around the original orbit rather than diverging away from it. Stability is a more general concept that can apply to both bound and unbound orbits.

Now, as it turns out, there exist only two types of central force potentials that produce closed orbits for all bound particles: the inverse-square law potential ( $V(r) \propto -1/r$ ) and the radial harmonic oscillator potential ( $V(r) \propto r^2$ ). This result is known as Bertrand’s theorem.

As far as stability is concerned, all closed orbits must be stable to begin with. Hence, the inverse square law and radial harmonic oscillator potentials produce stable closed orbits.

Aside from these two, there are also closed circular orbits in any central force potential, but these are not stable in general. (in a potential $V(r) \propto r^n$ , circular orbits are stable only if $n > -2$ )

Daniel, a strange guy, finds a strange force as well. He finds it to be a central force proportional to $r^n$ , where $r$ is the distance from the source of the force to the body affected by it (perhaps, think of it as a strange type of “gravity”). What value of $n$ could make it such that closed, stable, nearly circular orbits can occur by bodies under the influence of this force (that is, orbits without precession each period)?

\text{A.} \: 10 \qquad\qquad \text{B.} \: 11 \qquad\qquad \text{C.} \: 12 \qquad\qquad \text{D.} \: 13

A central force proportional to $r^n$ would give a potential of the form

V = k r^{n + 1} = k u^{-n - 1}

Using the binet equation,

u'' + u = \frac{mk(n+1)}{L^2} u^{-n - 2}

Let the radius of a circular orbit be $u_0$ . For a circular orbit, $u'' = 0$ , which gives

u_0^{n + 3} = \frac{mk(n+1)}{L^2}

To check for stability, we perturb the orbit a little. Substituting $u = u_0 + \eta$ and linearizing (ignoring quadratic and higher order terms), we get

\eta'' + \eta = \frac{mk(n+1)}{L^2} (u_0^{-n - 2} \eta - (n + 2) u_0^{-n - 1} \eta)

This gives a linear equation for $\eta$ , which can be analyzed for stability.

\eta'' + (n + 3) \eta = 0

This is an equation for a simple harmonic motion. Thus for small perturbations, the orbit oscillates about the circular orbit with frequency $\sqrt{n + 3}$ . Therefore, for stability, we need $n + 3 > 0 \implies n > -3$ .

For the orbit to be closed, we must have that the frequency of oscillation is a rational multiple of the orbital frequency. The orbital frequency is 1 (since $\theta$ increases by $2\pi$ in one orbit), and the oscillation frequency is $\sqrt{n + 3}$ . Therefore, for closed orbits, $\sqrt{n + 3}$ must be a rational number.

The only option which satisfies both these conditions is $\textbf{D. 13}$ .

Precession of apasis in General Relativity

The orbit equation in general relativity is given by

\frac{d^2 u}{d \theta^2} + u = \frac{GMm^2}{L^2} + \frac{3GM}{c^2} u^2

Defining a dimensionless $w = \frac{L^2}{GMm^2} u$ and $\alpha = \frac{2G^2M^2m^2}{c^2L^2} \:\: (\ll 1)$ ,

\frac{d^2 w}{d \theta^2} + w = 1 + \alpha w^2

Since $\alpha$ is very small, we can use perturbation methods to find an approximate solution for $w$ . In the first order, $w (\alpha)$ can be expanded in terms of a power series as

w = w_0 + \alpha w_1

$w_0$ just gives the newtonian solution

\frac{d^2 w_0}{d \theta^2} + w_0 = 1 \implies w_0 = 1 + e \cos \theta

For $w_1$ , we get

\frac{d^2 w_1}{d \theta^2} + w_1 \approx w_0^2 = 1 + \frac{e^2}{2} + 2 e \cos \theta +\frac{e^2}{2} \cos 2 \theta

This gives the solution for $w_1$ as

w_1 = 1 + \frac{e^2}{2} + e \theta \sin \theta - \frac{e^2}{6} \cos 2 \theta

Putting everything together and neglecting the small terms, we get

w \approx 1 + e \cos \left[ (1 - \alpha) \, \theta \right]

The period of the ellipse is not $2 \pi$ , and hence precesses at a rate of

\Delta \varphi = \frac{2 \pi}{1 - \alpha} \approx 2\pi (1 + \alpha) = \frac{2\pi G^2 M^2 m^2}{c^2L^2}

which matches the result which we obtained via the precession of the LRL vector. This apsidal precession is prominent in the orbit of Mercury.

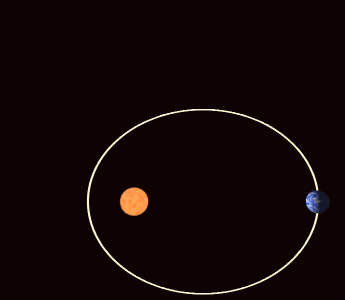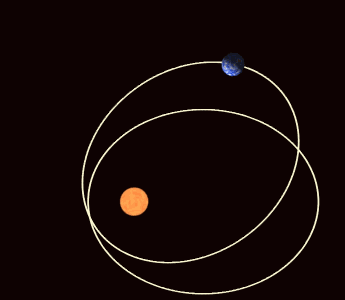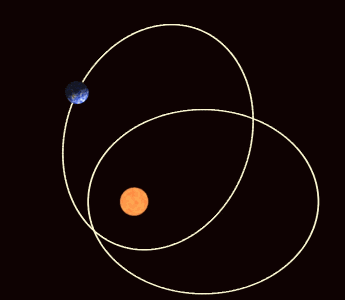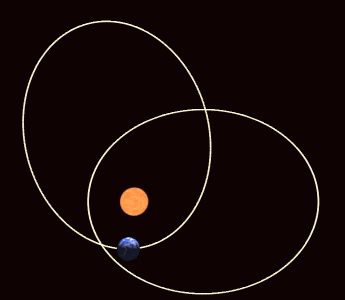
Precession of apsis in General Relativity

The apsis of the orbit precesses over time if considering effects of general relativity. (Source: Wikipedia)

Orbits in General Relativity

As shown earlier, elliptical orbits in general relativity tend to precess. The energy conservation equation is given by

\frac{1}{2} \dot{r}^2 + \frac{h^2}{2r^2} - \frac{GM}{r} - \frac{GMh^2}{c^2 r^3} = \epsilon

where the central body of mass $M$ is much more massive than the orbiting body of mass $m$ and is essentially at rest. Here $\epsilon$ is a term related to the energy of the system, and $h$ is the specific angular momentum of the orbiting body. For a circular orbit, $\dot{r} = 0$ , which gives the radius of the orbit as

\tag{3.7.9} r = \frac{h^2}{2GM} \left[ 1 \pm \sqrt{1 -\frac{12G^2M^2}{c^2h^2}} \right]

We see that for a given angular momentum $h$ , two circular orbits are possible. Introducing $a = h/c$ and the schwarschild radius $r_s = \frac{2GM}{c^2}$ ,

r = \frac{a^2}{r_s} \left( 1 \pm \sqrt{1 - \frac{3r_s^2}{a^2}} \right)

Therefore for a circular orbit, $a > \sqrt{3} r_s$ . This puts a limit on the minimum angular momentum of the body.

The inner orbit

r_\text{inner} = \frac{a^2}{r_s} \left( 1 - \sqrt{1 - \frac{3r_s^2}{a^2}} \right)

is unstable, while the outer orbit

r_\text{outer} = \frac{a^2}{r_s} \left( 1 + \sqrt{1 - \frac{3r_s^2}{a^2}} \right)

is stable. Therefore the minimum radius of a stable circular orbit is when $a^2 = 3r_s^2$

\tag{3.7.10} r = \frac{a^2}{r_s} = 3r_s = \frac{6GM}{c^2}

In the limit $a \gg r_s$ ,

\tag{3.7.11} r_\text{outer} = \frac{2a^2}{r_s} = \frac{h^2}{GM}\,,\qquad\qquad r_\text{inner} = \frac{3}{2} r_s = \frac{3GM}{c^2}

Circular orbits with radius smaller than $\frac{3}{2} r_s$ are not possible. For massless particles (photons), the only circular orbit possible is at $r = \frac{3}{2} r_s$ .

Gravitational Waves

Consider two massive bodies $M_1$ and $M_2$ orbiting each other, with position vectors $\mathbf{r_1}$ and $\mathbf{r_2}$ relative to the center of mass. We define $M = M_1 + M_2$ and $m = \frac{M_1 M_2}{M_1 + M_2}$ .

According to general theory of relativity, accelerated masses with non zero quadrouple moments radiate gravitataional waves (GWs) and lose energy. For small enough velocities, the emitted GWs

have a frequency twice as large as the orbital frequency
can be characterized by a luminosity, which is dominated by the expression

\tag{3.7.12} P = \frac{32}{5} \frac{G}{c^5}m^2 a^4 \Omega^6

where $a$ is the orbital separation and $\Omega$ is the angular velocity of each mass.

The energy of the system is $E = - \frac{GMm}{2a}$ . Differentiating, we get

\tag{3.7.13} \left( \frac{d \Omega}{dt} \right)^3 = \left( \frac{96}{5} \right)^3 \frac{\Omega^{11}}{c^5} (GM_c)^5

where we define the chirp mass $M_c = m^{3/5} M^{2/5}$ .

Now, $f_\text{GW} = 2f = \frac{\Omega}{\pi}$ gives

\tag{3.7.14} f_\text{GW}^{-8/3} (t) = \frac{(8 \pi)^{8/3}}{5} \left( \frac{GM_c}{c^3} \right)^{5/3} (t_0 - t)

where $t_0$ is a constant of integration.

Poynting Robertson Effect

The force of radiation acting on a particle of mass $m$ density $\rho$ and radius $R$ is $F_\text{rad} = P_\text{rad} \sigma_\text{pr}$ , where $\sigma_\text{pr} = Q_\text{pr} \pi R^2$ is the cross section of the particle, $Q_\text{pr}$ is the radiation pressure coefficient, and $P_\text{rad}$ is the radiation pressure. The radiation pressure is given by

\tag{3.7.15} P_\text{rad} = \frac{L}{4 \pi r^2 c}

where $L$ is the luminosity of the star and $r$ is the distance from the star. For sun, the peak wavelength is $\lambda_{p} \approx 500 \mathrm{\,nm}$ . For $R \gg \lambda_p$ , where sun’s gravity dominates over radiation pressure, the Poynting-Robertson effect acts as a brake on orbiting particles, decreasing their angular momenta so that they slowly spiral into the sun. In the frame of the orbiting particle, the phenomena of abberation causes slight displacement in the direction of the motion for photons striking the particle. This applies a torque on the particle, causing it to lose angular momentum.

\mathbf{\tau} = \mathbf{r} \times \mathbf{F} = \frac{d \mathbf{L}}{dt}

\tau = -rF_\text{rad} \sin \theta = -r \frac{LR^2 Q_\text{pr}}{4cr^2} \frac{v}{c}

The angular momenta of the orbiting particle is

L = m \sqrt{GMr} \implies \frac{dL}{dt} = \frac{m}{2} \sqrt{\frac{GM}{r}} \frac{dr}{dt}

Hence we get that the radius of the particle’s orbit decays as

\frac{dr}{dt} = -\frac{1}{r} \frac{L}{2c^2} \frac{R^2 Q_\text{pr}}{m}

The Poynting Robertson time scale is the time it takes for the particle to spiral into the sun

\tag{3.7.16} t_\text{pr} = \frac{a^2 c^2}{L} \frac{4 \pi}{3} \frac{\rho R}{Q_\text{pr}}

where $r = a$ is the initial radius of the particle’s orbit.

Orbital Maneuvers